When we measure anything, the resulting measurements are often referred to as variables or dimensions. For example, a cube has three dimensions that can be measured: length, width and height. When we measure a complex sample using mass spectrometry (like a proteome, metabolome or food sample), we measure the molecules as mass features at specific retention times. Then we transform this information into compound identifications with quantitative values through various methods. So each measured protein/small molecule (whether it is the m/z-RT level information or the analyte-quant level information) can be considered to be a dimension of that sample. In this respect, a metabolome with 5000 quantified molecules has 5000 dimensions.
When measuring complex samples, we expect a suite of dimensions (proteins, small molecules, m/z-RT pairs) to have large variation in their abundance across the total sample population – meaning that abundance is low in some samples and high in others for at least some dimensions.
As an example, in a perfectly controlled experiment with two sample groups, we expect that the dimensions with large variation will relate to the biological differences between the two groups. As such, it is often of interest to see how the overall variation in a sample population relates to the experimental groups.
We can easily visualize up to three dimensions (e.g. with a x-y-z plot), but any more than three can be difficult to visualize and interpret in a meaningful way. Even if we filter MS data to focus only on dimensions that have large variation, very often we are still faced with more than three dimensions to interpret. In reality, there are often more than 100 differential dimensions to consider! Furthermore, if we filter down to only a few dimensions, we might overlook information that is important to the biology under examination. In this respect, it can be desirable to consider all sample dimensions while still reducing the complexity of the data.
Principal component analysis (PCA) is a data transformation technique that can be used to reduce the complexity of high-dimensional data sets (such as mass spectrometry data) while retaining most of the variation in the data set.
Through this transformation, PCA allows users to readily plot the overall variation found within multi-dimensional data using only two or three new dimensions. This provides a simple way to visualize the overall structure of complex data (e.g. clustering), while identifying the key features (proteins/small molecules) that are responsible for such structure.
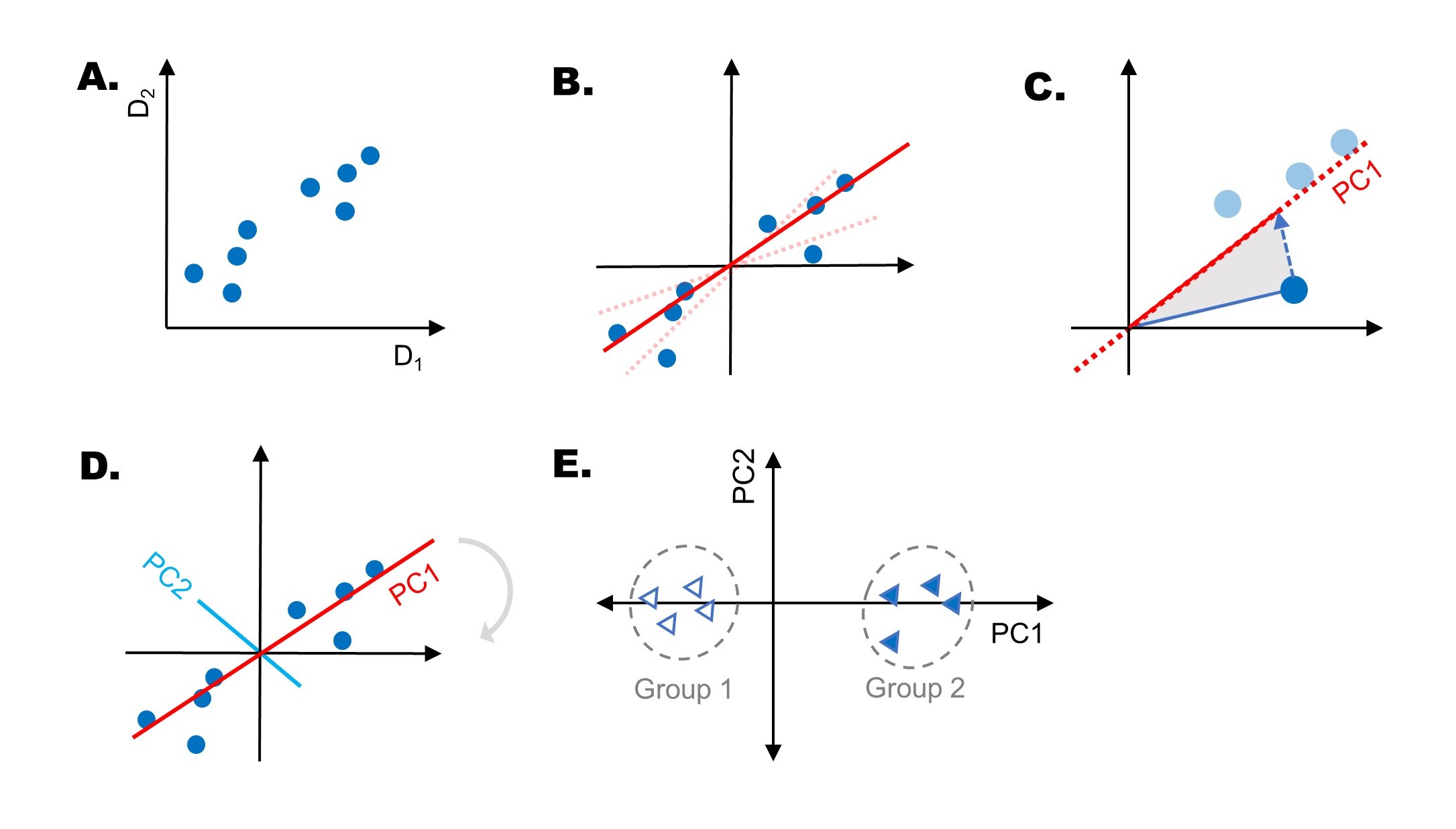
For a given set of dimensions D1, D2…(A), principal component analysis models a line of best fit (B), and minimizes the sum of squared distances of the points to the line. The line with the smallest sum of squared distances is called PC1, and is a linear combination of dimensions D1 and D2. This variance is sometimes called the eigenvalue of PC1. For the special case of two dimensions this is equivalent to a standard linear regression.
The calculated unit vector of PC1 (also called the eigenvector) is used to calculate the relative proportion of D1 and D2; we call these Loadings. These loadings tells us how important each dimension is to PC1, and can be used to determine the proportion of variation each PC describes. (C). This process is repeated for each principal component, with PC2 drawn perpendicular to PC1 (D). The two principal components that describe the largest variation in the data can be visualized on a two-dimensional plot, by rotating the axes until PC1 is horizontal (E).
Principal components are calculated in order of the amount of variance they explain. For each principal component every sample has a score and every variable has a loading which indicate how important it is for that principal component. Multiple different principal components can be calculated for a given dataset; for simplicity, MarkerView software stops the calculation when the amount of variance explained by a principal component is < 0.5% of the total.
For this set of MarkerView software posts, we will use an example data set collected by analyzing the urine from three rats administered a single dose of vinpocetin (closed circles) or vehicle control (open squares). Samples were collected at three different time points (2h, blue; 8h, red; and 16h, green), for a total of 18 samples. You can find a copy of the data with your install of MarkerView software 1.3.1 under the following directory:
C:\Program Files (x86)\SCIEX\MarkerView 1.3\Sample Data\LCMS Data
The matching plot symbols can be downloaded here. To import, click Edit > Options, and select the “Import” option from the Plot Symbols tab, then navigate to the downloaded .ptsym file.

The image below shows the Scores (left) and Loadings plots (right) for PC1 and PC2 for our example rat data, consisting of six experimental groups, described above.
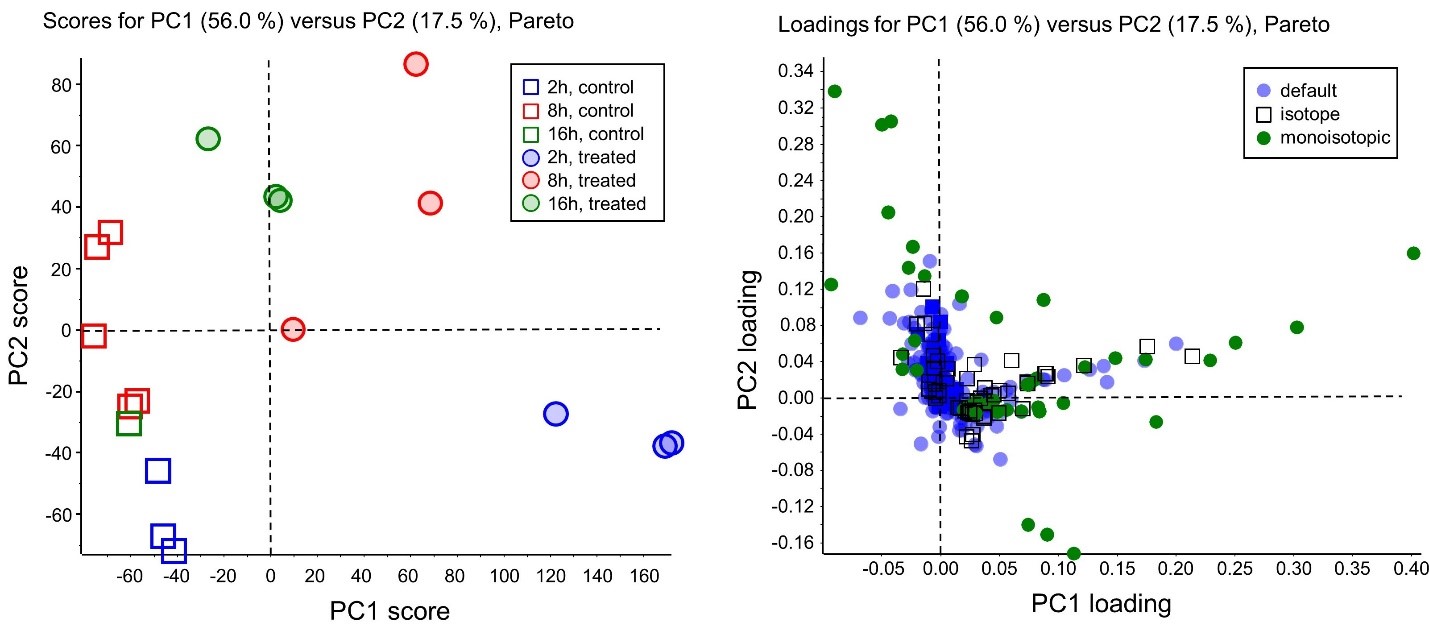
It is important to remember that the data structure might be independent of our assigned experimental groups if there are other large sources of variation in the data (e.g. technical variation between replicates). This is because PCA is an unsupervised technique, meaning that it does not consider the experimental grouping of your samples when performing a data transformation. To identify dimensions that can discriminate between experimental groups refer to principal component analysis – discriminant analysis (PCA-DA).
If you really want to dig in, here are some useful references:
- Ringner M. What is Principal Component Analysis? (2008) Nature Biotechnology 26, 303-304.
- MarkerView software user guide – MarkerView software reference guide – C:\Program Files (x86)\SCIEX\MarkerView 1.3\Help
RUO-MKT-18-12137-A



 Contact Support
Contact Support
0 Comments