A t-test (sometimes called Student’s t-test) is used to determine if the means of two sample groups are significantly different. So, for LC-MS data, we would typically use a t-test to find out if the amount of our variable of interest (protein, peptide, small molecule, or m/z + retention time combination) is different between experimental groups.

When using a t-test, we assume that the underlying data has a normal distribution, and our experimental groups are of equal size, with equal variance. If the two samples have unequal variances and unequal sample size, we should use the Welch t-test. This option can be selected from the t-test dialog box.

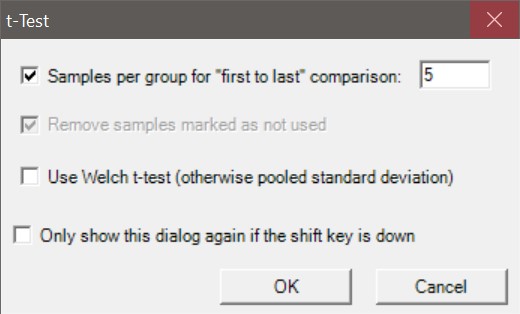
The reason for this is that unequal variances can alter the Type I error rate. That is, we might falsely reject the null hypothesis and report a significant difference of means where no true difference exists. The more unequal the variance of the two populations, the greater the Type I error rate. ¹ Therefore, it is important to use the Welch t-test if it is appropriate for your data.

Non-parametric tests (i.e. for data that does not have a normal distribution) are not supported in MarkerView software. Fortunately, the shape of the distribution has little impact on the Type I error rate, and for studies with a large sample size, t-tests can be used even for skewed data.^1,2

Once you have defined your experimental groups in MarkerView software (via the Samples table), you can perform the t-test and it will automatically compare all groups in pairs. A new pane will open with a table containing p- and t-values, plus profile and box-and-whisker plots. There will be more on that later.

The t-value is a measure of how well the variable distinguishes between two groups. Conversely, the p-value is the probability that the delta value would occur by chance. If the value of t exceeds a calculated critical value then the variable does distinguish the groups with some confidence value; t can be positive or negative depending on the direction of the subtraction of the means. The p-value is always positive and the smaller the value, the lower the probability that this is a chance occurrence.

The best way to visualize these results is to plot the p-value computed for each variable versus its log fold change. This is known as a Volcano plot and allows you to see both how large and how significant the specific variable is in distinguishing between the two groups. The example on the left is from our rat dataset. Notice that there are relatively few data points on the plot. This is because we are using a simplified data set for the purposes of this tutorial series. A volcano plot from a “real data” set is shown on the right. This example compares blood samples taken from turtles living in two geographial locations.³

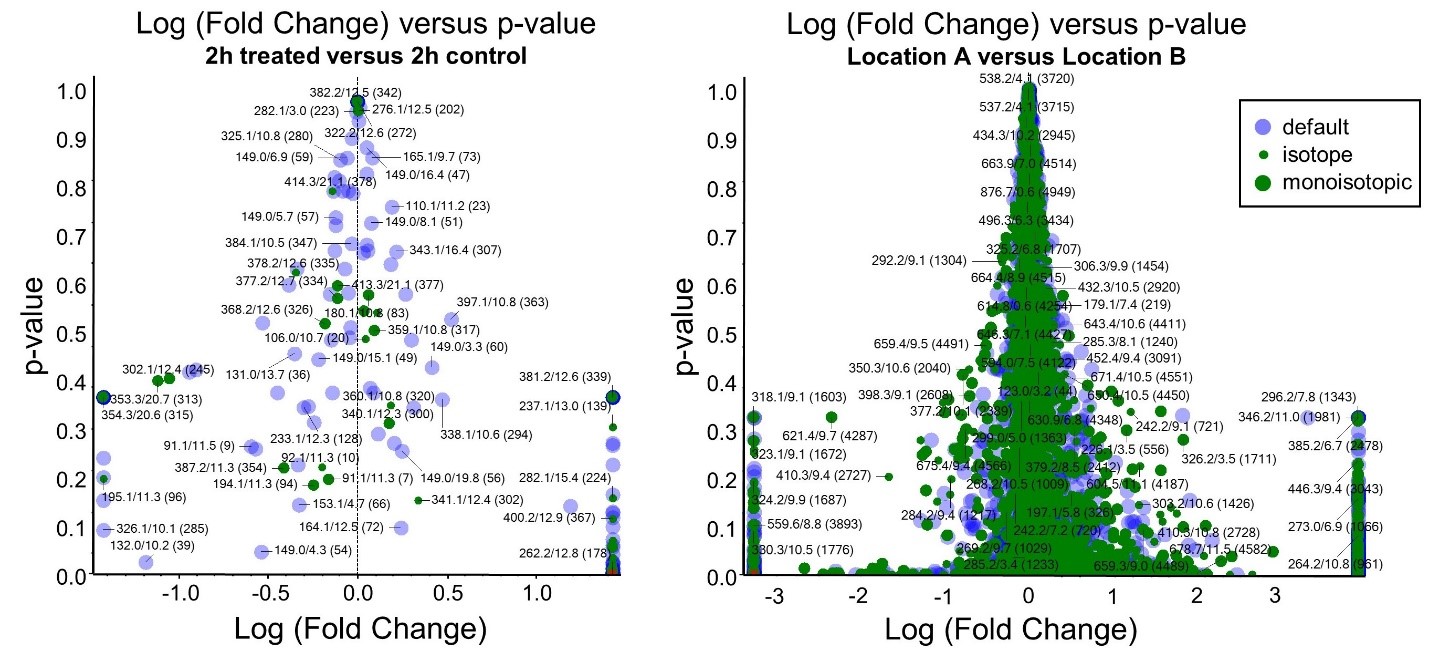
Let’s revisit our rat example.

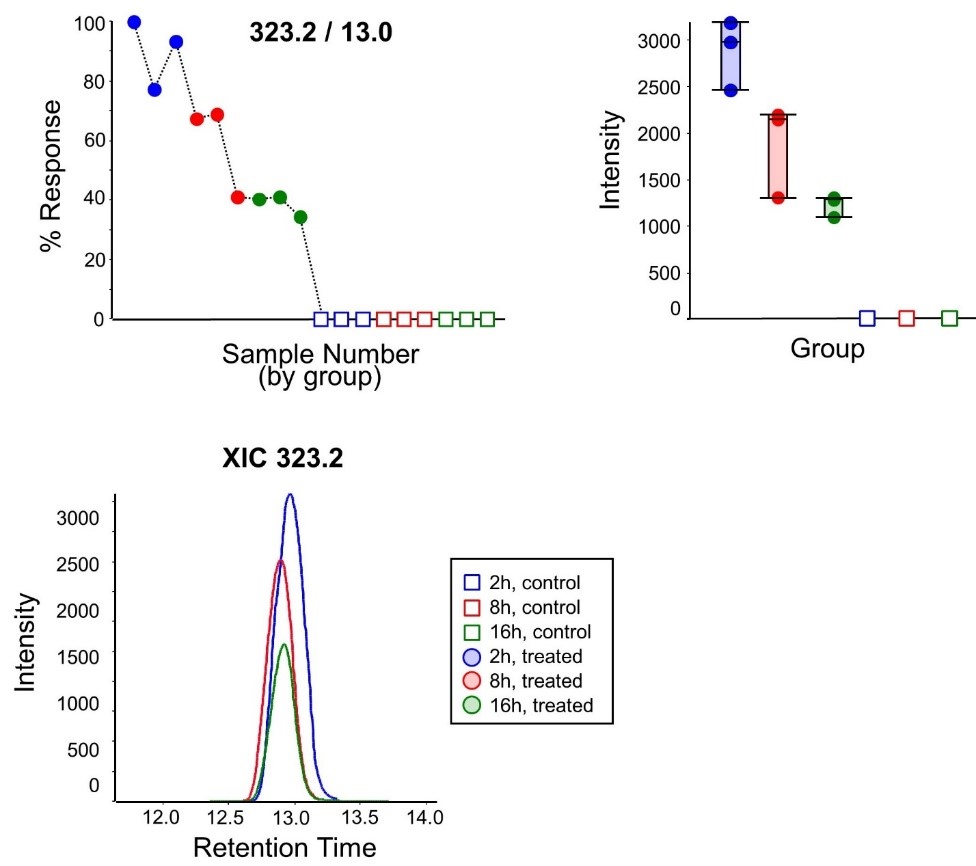
When we select the most extreme feature from the volcano plot (m/z 323.22 at 13.0 min), we can generate a profile plot for our 18 samples (top left), and a box-and-whisker plot (top right) for our experimental groups. It is clear that this variable is absent from the control samples, and exhibits a time-dependent decrease in response post-administration. By highlighting specific samples in the profile plot, we can also review extracted ion chromatograms (XICs) and spectral information for the selected samples via the right-click menu. At this stage of the workflow, we can choose to add a feature to an “Interest List” and import it into SCIEX OS Software for compound identification.

Helpful references:

1. Delacre, M et al. (2019) “Taking Parametric Assumptions Seriously: Arguments for the Use of Welch’s F-test instead of the Classical F-test in One-way ANOVA.” International Review of Social Psychology. 32(1):13.
2. Fagerland M. W. (2012) “t-tests, non-parametric tests, and large studies–a paradox of statistical practice?”. BMC Medical Research Methodology, 12:78.
3. Heffernan A. L. et al. (2017). “Non-targeted, high resolution mass spectrometry strategy for simultaneous monitoring of xenobiotics and endogenous compounds in green sea turtles on the Great Barrier Reef.” Sci Total Environ 599–600: 1251-1262.

RUO-MKT-18-12137-A